Ezúttal a sokak által egyetlen hazai likvid papírnak nevezett OTP kerül górcső alá, egészen pontosan abból a perspektívából, hogy mi az általános (már-már közmondásnak tartott) vélekedés az árfolyammozgást kiváltó faktorokról. Ez a gondolkodás egyúttal arra a kérdésre is megpróbál választ adni, hogy mely kereskedési stratégia lehetett sikeres a múltban. Az alábbiakban három kiragadott témakör köré igyekszem csoportosítani mondanivalómat.
Amerikai indexek
A nagy többség elsődlegesen a mértékadó amerikai tőzsdeindexek (S&P500 és Dow Jones) alakulását igyekszik figyelemmel követni.
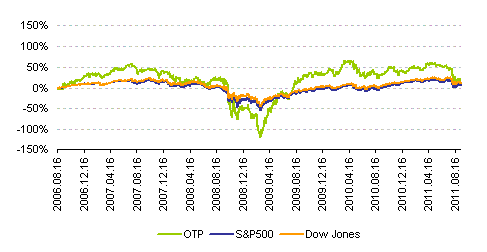 |
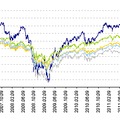
| Kumulált napi hozamok alakulása az elmúlt öt évben |
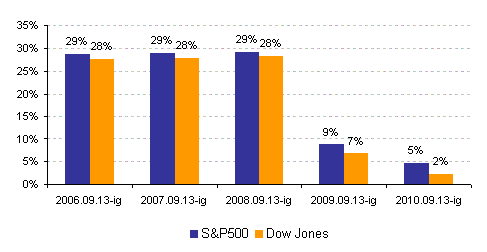 |
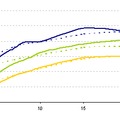
| Korreláció 1: Az OTP előző napi záró és adott napi nyitó árfolyamainak különbsége vs. amerikai indexek napi hozamai |
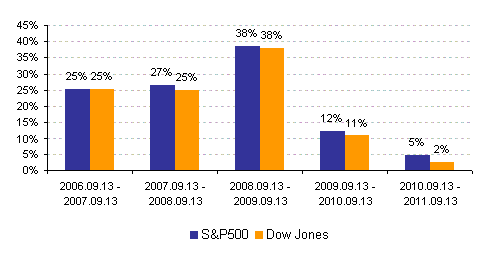 |
| Korreláció 2: Az OTP előző napi záró és adott napi nyitó árfolyamainak különbsége vs. amerikai indexek napi hozamai |
Az ábrák alapján három főbb megállapítás mondható el. Először is a korrelációs együtthatók mindvégig pozitív kapcsolatot írtak le. Továbbá a 2008-2009-es globális pénzügyi válság szignifikánsan erősítette az együttmozgást, ugyanakkor érdekes módon 2009 második negyedévétől trendszerűen gyengült a kapcsolat (s már-már a nullához közelít - gyakorlatilag egyre kevésbé hordoznak extra információt a tengerentúli zárók).
Devizaárfolyamok
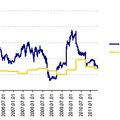
Lássuk, mi a helyzet a CHF/HUF és az EUR/HUF keresztekkel az OTP vonatkozásában.
 |
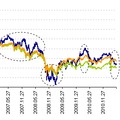
| Korreláció 3: Az OTP adott napi hozamai vs. EURHUF és CHFHUF napi hozamai |
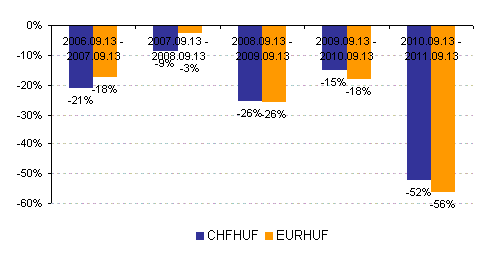 |
| Korreláció 4: Az OTP adott napi hozamai vs. EURHUF és CHFHUF napi hozamai |
Több éves időhorizonton számottevő magyarázóerővel (közepesen magas negatív korreláció) bír a vonatkozó devizaárfolyamok alakulása, első ránézésre jól kereskedhetőnek tűnik, ám az előbbi ábra jól mutatja, hogy ez a hatás leginkább csak az elmúlt egy év eredménye.
Együtthatások
A következőkben arra keresem a választ, hogy az eddig bemutatott változók hozamai együttesen milyen magyarázóerővel rendelkezhet az OTP hozamokra. Ennek az elemzésnek egyik kézzelfogható eszköze a lineáris regresszió, melyet a teljes 2006.08.16 - 2011.09.13 közötti időszakra használtam.
| mind a négy változó időbeli késleltetés nélkül | csak a két devizaárfolyam időbeli késleltetés nélkül | mind a négy változó, az indexek egy napos késleltetéssel | |
| tengelymetszet | 0,000078 | 0,000166 | 0,000156 |
| S&P500 | 0,106670 | 0,321241 | |
| Dow Jones | 0,460431 | 0,119828 | |
| HUFCHF | 0,225414 | 0,649260 | 0,698231 |
| EURHUF | -0,938932 | -0,968990 | -0,963646 |
| R^2 | 0,246902 | 0,198717 | 0,246385 |
| standard hiba | 0,022875 | 0,023583 | 0,022888 |
Gyakorlatilg állandó becslési hiba mellett mindvégig gyenge magyarázóerővel bíró modelleket kaptunk, mely elveti annak lehetőségét, hogy efféle "egyszerű" módon jövőbeli előrejelzésre használjuk ezeket a többváltozós lineáris egyenleteket (ugyanakkor némiképp figyelemreméltó az euróárfolyamból számolt napi hozamok együtthatójának állandósága). Természetesen az imént bemutatottnál jóval összetettebb (még több változó, nem lineáris keretek stb.) egyetemi dolgozat szintű modellek építhetők, az pedig ezen gondolatindító rövid bejegyzés keretein túlmutat.